4.2        OLCR measurement of the complex impulse response

4.2.3       Propagation in vacuum

a)   Michelson interferometer example

A free-space Michelson interferometer can be used as a simple experimental method for measuring g(t) (Fig. 4-3a). The light source (L) with its spectrum centered at 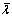emits the stationary electric field E_s(t). The test (M_test) and reference mirrors (M_ref) are placed at a distance h₁ and h₂ respectively from the beam splitter (BS). The signals back-reflected from reference and test arms E_ref and E_test interfere at the detector (D).

Fig. 4-3 Free-space Michelson interferometer set-up (a) and simulated interferogram (b)

We consider perfects mirrors with 100 % reflectivity coefficients and a 3 dB beam splitter (these assumptions influence only the constant coefficients). In this case, the reference and test intensities are identical and equal to a forth of the light source intensity I_s. The light propagation constant in vacuum is k = 2pn/c₀, c₀ = 3×10⁸ m/s is the light speed in vacuum and then

where the electric field is decomposed in its frequency components E_n, t₂ = (2h₂)/c₀ is the time needed for all frequencies to travel a distance 2h₂ and w  = 2pn is the light angular frequency. It is important to note that the time t₂ becomes frequency dependent if the light does not propagate in vacuum as the propagation constant becomes b(n) = n(n)×k, where n(n) is the refractive index. In this case, equation (4-11) is not valid anymore. This point will be discussed in section 4.2.4 with the introduction of the group velocity in dielectric materials. For the test signal, a similar expression is obtained with E_test(t) = E_s(t+t₁)/2 where t₁ = (2h₁)/c₀. Small algebraic manipulations show that the interference signal I(h₁,h₂) is

and only depends of the factor t = t₂-t₁. The factor difference of 4 between equations (4-10) and (4-12) is due to the beam splitter.

The typical normalized interferogram 2I/I_s = 1+Re(g) is shown in Fig. 4-3b. We observe a maximal signal for t = 0 with constructive interference. Then the signal drops symmetrically and the first destructive interferences occur at a distance mismatch of 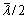(the factor 2 is due to the back and forth travel distance). Then other constructive and destructive interferences are observed but with a decreasing amplitude |g|. Side-lobes are also observed and fully explained by the Fourier transform of the source power spectral density. For a Gaussian light source described by a Gaussian function, S(n), the degree of coherence envelope |g| is also a Gaussian function and side-lobes are totally suppressed.